◎新潟駅・東三条駅・六日町駅・長岡駅・上越高田駅・仙台駅の塾、真友ゼミの講師陣による大学受験勉強方法ブログ！

先日、生徒と面談をしていたら

「化学の気体の分野の問題あるじゃないですか。問題が単純なら解けるのですが、複雑になると訳わからなくなってしまって…」

という話がありました。
この話を聞いて「理論化学の得点源なのに苦手意識をもって解けないままにしておくなんてもったいない！！」と思ったので、気体の分野の問題の解き方のコツを紹介します！

気体の状態方程式～勉強方法のポイント～

まず覚えるべき公式は気体の状態方程式(PV=nRT)だけでいいです！

ボイル・シャルルやアボガドロの法則は覚える必要はありません。
状態方程式の中で定数をまとめてkとおくことにより、ボイル・シャルルもアボガドロもすべて立証できます。

気体の問題を攻略するために必要なポイント…それは「問題文を図示せよ！」という点につきます。
問題文からいきなり式に代入すると、『一定』のものと『変数』のものを見間違えるのでオススメしません(乂’ω’)

また反応によっては化学反応式を伴うものもあるので、イメージを可視化することも大切です。

もう１つの状態方程式も導き出すとかではなく、暗記しておくと便利な式を紹介します！

その状態方程式がPM=dRTです。(M：分子量,d：密度)

モル数n=w(質量)/M（分子量）です。
そこに、これを代入して

PV=wRT/Mとなります。 

この式に両辺Mを掛けて、Vで割ります。

するとPM=(w/V)RTとなります。

(w/V)は単位体積辺りの質量だから、これは密度dです。よってPM=dRTとなります。

では最後に具体例を見ながら説明していきます。

【問題】27℃, 1.00×10⁵ Paにおいて気体である物質Xの密度を測定したところ1.2 g/Lであった。1mol気体定数8.3×10³(Pa・L)/(mol・K)であるとき、この気体Xの分子量を求めよ。

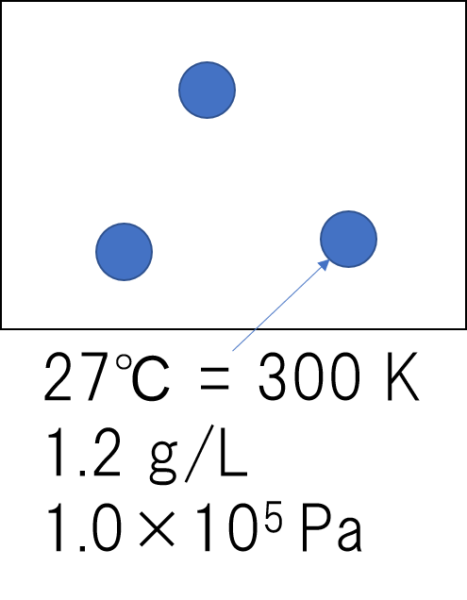
気体の粒までしっかり描きましょう。
この粒の数がモルの変化をしているかどうかを表現するのに重要だからです。

先ほど変形したPM=dRTを利用して解くと、

M=dRT/P=1.2 (g/L)×8.3×10³(Pa・L)/(mol・K)×300(K)÷1.0×10⁵(Pa)=29.88≒30

今回紹介した問題はシンプルでわかりやすいものですが、実際は混合気体になっていたり、水に溶かしてみたり…と様々な操作を行っています。

どんな問題だったとしても、変わるものと変わらないものを見極めることが重要です！
なので複雑な問題ほど図示して何の値が一定で何の値が変数なのか、はっきりさせていくことを意識しましょう！